المنطق

الرموز الرياضياتية المُستعملة في هذا الدرس

طــ: مجموعة الأعداد الصحيحة الطبيعية

صـ: مجموعة الأعداد الصحيحة

كـ: مجموعة الأعداد الكسرية

حـ: مجموعة الأعداد الحقيقية

العبارة

العدد 1 عدد كسري. نص رياضي يحمل معنى صحيح (ص)٠

العدد 2√ عدد كسري. نص رياضي يحمل معنى خاطئا (خ)٠

المكممات

يوجد على الأقل عدد كسري ، 0 < خ < 1 . ونرمز لهذه العبارة بِـ ∃ س∈ كـ ، 0 < خ < 1 ٠ :∃

 يوجد عدد صحيح طبيعي خ وحيد أكبر قطعا من 0  و أصغر  قطعا من 2 :!∃
ونرمز لهذه العبارة بِـ ∃! س ∈ طـ ، 0 < خ < 2 ٠

مهما يكن العدد الحقيقي س، فإن مربع العدد س عدد موجب :∀
ونرمز لهذه العبارة بِـ ∀ س ∈ حـ، س²  ≥ 0  ٠ 

ملاحظة

في نص رياضي ترتيب المكممات جد مهم

العمليات المنطقية: النفي المنطقي؛ الفصل و العطف المنطقي؛ الاستلزام المنطقي؛ التكافئ المنطقي

النفي المنطقي

مثال

 نعتبر العبارة (عـ) ∃ س ∈ حـ ، س²+ 2 س + 5 = 0، هذا النص الرياضي يعني أن المعادلة تقبل حلا على الأقل في مجموعة الأعداد الحقيقية حـ ٠

لكن المعادلة ليس لها حل في مجموعة الأعداد الحقيقية حـ لأن مميزها سالب قطعا، و هذا يمكن التعبير عنه بِـ : ∀ س ∈ حـ ، س² + 2 س + 5 ≠ 0

هذا النص الجديد يسمى نفي العبارة (عـ) ونرمز له بِـ (¬عـ) ٠

قاعدة

نفي العبارة ∀س∈ : هـا(س) هي العبارة ∃س∈ : ¬هـا(س) ٠

نفي العبارة ∃س∈ : هـا(س) هي العبارة ∀س∈ : ¬هـا(س) ٠

مثال

نفي العبارة ∀س∈حـ ، س + 1 ≥ 0 هي العبارة ∃س∈ حـ ، س + 1 < ٠0

الفصل و العطف المنطقي

تكون العبارة ((عـ1) أو (عـ2)) صحيحة اذا كانت على الأقل احدى العبارتين (عـ1) أو العبارة (عـ2) صحيحة، ونرمز له بِـ (عـ1) ∧ (عـ2)٠

تكون العبارة ((عـ1) و (عـ2)) صحيحة اذا كانت العبارة (عـ1) و العبارة (عـ2) صحيحتان معا، ونرمز له بِـ (عـ1) ∨ (عـ2)٠

ملاحظة

نفي العبارة (عـ1 أو عـ2) هي العبارة (عـ1 و عـ2) ٠

نفي العبارة (عـ1 و عـ2) هي العبارة (عـ1 أو عـ2) ٠

ملاحظة

في بعض النصوص الرياضية ، يكون الفصل مخفيا. مثلا

س عدد حقيقي، الكتابة س ≥ 1 تعني (س = 0 أو س > 1 ) ٠

الإستلزام المنطقي

مثال

نعلم أن كل عدد صحيح طبيعي مضاعف للعدد 4 هو مضاعف للعدد 2 ٠

يمكننا صياغة ذلك كما يلي: ص عدد صحيح طبيعي مضاعف للعدد 4 ، إذن ص عدد صحيح طبيعي مضاعف للعدد 2 ٠

نقول أن العبارة (عـ1) "ص عدد صحيح طبيعي مضاعف للعدد 4" تستلزم العبارة (عـ2) "ص عدد صحيح طبيعي مضاعف للعدد 2"٠

ونكتب (عـ1) ⇐ (عـ2) ٠

بصفة عامة ليكن عـ1 و عـ2 عبارتين

نقول أن العبارة (عـ1) تستلزم العبارة (عـ2) و نرمز لها بالكتابة (عـ1) ⇐ (عـ2) عندما تتحقق إحدى الحالات

العبارة (عـ1)صحيحة و العبارة (عـ2) صحيحة

العبارة (عـ1) خاطئة و العبارة (عـ2) صحيحة

العبارة (عـ1) خاطئة و العبارة (عـ2) خاطئة

مثال

العبارة ( ن عدد صحيح طبيعي زوجي ⇐ ن + 2 عدد زوجي) عبارة صحيحة

العبارة ( 1 عدد زوجي ⇐ 2 عدد زوجي) عبارة صحيحة

العبارة ( 1 عدد زوجي ⇐ 3 عدد زوجي) عبارة صحيحة

العبارة ( ن عدد صحيح طبيعي زوجي ⇐ ن + 1 عدد زوجي) عبارة خاطئة

ملاحظة

العبارة (عـ1⇐ عـ2) تكون خاطئة فقط إذا كانت عـ1 صحيحة و عـ2 خاطئة

ملاحظة

ليكن (عـ1) ⇐ (عـ2) استلزاما صحيحا٠ فإن (عـ1) شرط كافي لِـ (عـ2) ، و (عـ2) شرط لازم لِـ (عـ1) ٠

الاستلزام المضاد للعكس

الاستلزام (¬عـ2) ⇐ (¬عـ1) يسمى الاستلزام المضاد للعكس للاستلزام (عـ1) ⇐ (عـ2)٠

التكافئ المنطقي

العبارة (عـ1) ⇐ (عـ2) و (عـ2) ⇐ (عـ1) تسمى تكافؤ العبارتين (عـ1) و (عـ2) ٠

ونكتب (عـ1)⇔(عـ2) ٠

و نقرأ (عـ1) تكافؤ (عـ2) ٠

ملاحظة

العبارة (عـ1 ⇐ عـ2) و العبارة (¬عـ1 أو عـ2) لهما نفس قيم الحقيقة، من هنا نستنج

أن العبارة (عـ1 ⇐ عـ2) تكافؤ العبارة (¬عـ1 أو عـ2) ٠

ثم نفي العبارة (عـ1 ⇐ عـ2) يكافؤ العبارة (عـ1 و ¬عـ2) ٠

الإستدلال المنطقي: الإستدلال بالخلف؛ الإستدلال بفصل الحالات؛ الإستدلال بالاستلزام المضاد للعكس؛ الإستدلال بالترجح

الإستدلال بالخُلف

إذا اردنا البرهان على صحة عبارة ما، نفترض أنها خاطئة و نحاول أن نجد تناقضا أو عبارة غير صحيحة٠

مثال:  المماس للدائرة يكون عموديا على نصف القطر المار بنقطة التماس٠

نبدأ البرهان بفرض أن المماس ليس عموديا على نصف القطر وبالسير بالمناقشة

 الصحيحة نأتي إلى أن المماس يقطع الدائرة في نقطتين وبما أن النتيجة تتعارض مع تعريف المماس، ينتج أن الإفتراض ليس صحيحا ويكون المماس عموديا على نصف القطر المار بنقطة التماس٠

مثال

 لتكن س عدد صحيح بحيث س² عدد عدد زوجي٠ بين أن س  عدد زوجي٠

نفترض أن س عدد فردي ، أي ∃ ش ∈ صـ بحيث س = 2ش + 1، س² = ...، إذن س² عدد فردي٠ و هذا يناقض المعطيات، إذن الإفتراض ليس صحيحا و بالتالي نفيه صحيح أي أن س عدد زوجي٠

الإستدلال بفصل الحالات

مثال

حل في حـ المعادلة: |س−3 | = 2 ٠

الحالة الأولى: س ≥ 3 ..... ٠

الحالة الثانية: س < 3 ..... ٠

الإستدلال بالاستلزام المضاد للعكس

العبارة ((عـ1) ⇐ (عـ2)) تكافؤ  العبارة ((¬عـ2) ⇐ (¬عـ1))٠

إذا اردنا البرهان على صحة العبارة (عـ1) ⇐ (عـ2) ٠

فإنه يمكننا عوضا عن ذلك أن نبرهن على صحة العبارة (¬عـ2) ⇐ (¬عـ1)٠

مثال

سنبين بالاستلزام المضاد للعكس بين أن: ∀ (س ،  ص) ∈ طـ ،  س² > 4 ⇐ ( س < −2 أو س > 2 )٠

لنبين عوضا عن ذلك أن (س ≥ −2 و س ≤ 2) ⇐ س² ≤ 4 ٠

أي −2 ≤ س ≤ 2 ⇐ س²  ≤ 4 ٠

بالفعل −2 ≤ س ≤ 2 ⇐ |س| ≤ 2 ⇐ |س|² ≤ 4 ⇐ س² ≤ 4 ٠

الإستدلال بالتراجح
لتكن ي_ن، عبارية متعلقة بِـ ن، بحيث ن عدد صحيح طبيعي، ن ≥ ن₀ 

لنبرهن على أن ي_ن، صحيحة لكل  ن ≥ ن₀

أولا نبين أن العبارة صحيحة عند الرتبة   ن₀

   ثانيا نفترض أن  العبارة صحيحة عند الرتبة ن٬ ثم نبين أن العبارة صحيحة عند الرتبة ن + ٠1

  مثال: ∀ ن ∈ طـ  3^ن  > ن
 أولا: نبين صحة العبارة عند الرتبة 0

 بما أن 1 > 0

  إذن العبارة صحيحة عند الرتبة 0

ثانيا: نفترض  صحة العبارة عند الرتبة ن٬  ثم نبين صحة العبارة عند الرتبة ن + 1 ٠

العبارة صحيحة عند الرتبة ن أي 3^ن   > ن

إذن 3^ن+1 > 3ن
بما أن  3ن  >  ن+ 1 إذن 3^ن+1  >  ن+ 1
إذن العبارة صحيحة عند الرتبة ن + 1 ٠

أي ∀ ن ∈ طـ   3^ن  > ن

ملاحظة

يمكن البرهان على تكافؤ باستعمال الاستلزام المزدوج٠

كي نثبت على صحة تكافؤ ((عـ1)⇔(عـ2)) يمكننا اثبات صحة الاستلزامين ((عـ2) ⇐ (عـ1)) و ((عـ1) ⇐ (عـ2))٠

مثال: س عدد صحيح زوجي تكافؤ س² عدد صحيح زوجي٠

(⇐) نين أولا صحة الاستلزام

س عدد صحيح زوجي أي ∃ ش ∈ صـ بحيث س = 2ش ،  س² = 4س² ، إذن س² عدد صحيح زوجي٠

(⇒) ثم نين صحة الاستلزام

أي س² عدد صحيح زوجي تستلزم س عدد صحيح زوجي٠

و نستعمل مثلا الإستدلال بالاستلزام المضاد للعكس: س عدد صحيح فردي ، أي ∃ ش ∈ صـ بحيث س = 2ش + 1، س² = ...، إذن س² صحيح عدد فردي٠

ملاحظة

كي نثبت على صحة التكافؤات (عـ1)⇔(عـ2) ⇔(عـ3) يمكننا اثبات صحة الاستلزامات (عـ1) ⇐ (عـ2) ⇐(عـ3) ⇐ (عـ1)٠

تمارين

تمرين1

بين أن كل عدد صحيح طبيعي و مربعه لهما نفس الزوجية٠

بين بالإستدلال بالخلف أن 2√ عدد غير كسري٠

تمرين2

مستعملا الاستلزام المضاد للعكس بين أن: ∀ (س ، ص) ∈ طـ ٬ س + ص < 2 ⇐ ( س≥1 أو ص≥1 )٠

تمرين3

بين بالتراجح أن: ∀ ن ∈ طــ  ٬  1 − 4ن مضاعف للعدد ٠3

تمرين4

 بين بالتراجح أن: ∀ س ∈ حـ  ٬ ( 1 + س +  س²  +  س³ ..... + س^ن ) ( 1  −  س² ) = ( 1  −  س^ن+1 )٠

تمرين5

ليكن ن عدد صحيح طبيعي٬ بين أن ن²  +  ن عدد زوجي٠

 ليكن س عدد حقيقي، بين أن إذا كان 2س + 1 مربعا كاملا فإن
س + 1 مجموع مربعين كاملين٠

 ليكن ن عدد صحيح طبيعي٬ بين أن العدد 1  −  9^ن يقبل القسمة على ٠8

عموميات حول الدوال، دوال ابتدائية

تمارين 

تمرين29
نعتبر الدالة العددية عا(س) =  س² – 2 س  – 1
أحسب صورة العدد 0
أحسب صورة العدد 1
حدد سوابق العدد – 2
أحسب صورة العدد –1
حدد سوابق العدد –1

بين أن التمثيل المبياني للدلة عـا يمر بالنقط: (0 ؛ ـ1) ، (ـ1 ؛ 2) ٬ (1 ؛ -2)٠

ادرس إشارة النسبة التالية٬ ثُم ارسم التمثيل المبياني للدلة عـا في المستوى منسوب إلى معــلم ممنظم و متعامد٠

ادرس جبريا و هندسيا تقاطع التمثيل المبياني للدلة عـا مع محور الأفاصيل٠

باستعملك للتمثيل المبياني للدلة عـا، اعطي صورة العدد 3، و سوابق العدد –٠1

تمرين30
دائرة الوحدة

بين أن الدوال المثلثية جب(س) (جيب) و تجب(س (جيب تمام) قيمها محصورة بين −1 و 1

و أن: جب² (س) + تجب² (س) =1 ، من أجل كل عدد حقيقي س

بين أن جب  و تجب دوال دورية، و أن  دورتهما تساوي 2ط

تمرين 31
لتكن عـا دالة معرفة على مجموعة الأعداد الحقيقية حـ
بحيث: لكل عددين حقيقيين س و ص، عـا (س + ص)  = عـا (س) + عـا (ص)٠
بيّن أن عـا (0) = 0 ، ثم استنتج بأن عـا دالة فردية٠
بيّن بأن لكل ن عدد صحيح نسبي، عـا (ن س)  = ن عـا (س)٠
بيّن بأن لكل كـ عدد كسري، عـا (كـ س)  = كـ عـا (س)٠
استنتج بأن عـا (كـ)  = عـا(1) كـ٠

الدرس

نظام الإحداثيات، معادلة الخط المستقيم

نظام الإحداثيات، المستقـيم الـمــدرج



المستقيم (اب) يسمى مستقيم مدرج، وتسمى النقطة ا نقطة الأصل، و طول القطعة [اب] وحدة الطول أو التدرج، نسمي النقطة ا نقطة الأصل
نسمي العدد 0 أفصــول النقطة ا و العدد 1 أفصــول النقطة ب
كل نقطة ن من المستقيم مرتبطة بعدد يسمى إحداثية النقطة ن٬ و نكتب : ن(س)

نظام الإحداثيات ثنائي الأبعاد، المعلم في المستوى



نعتبر (اب) و (ات) مستقيمين مدرجين على التوالي بواسطة [اب] و[ات] و متعامدين في النقطة ا٬ يسمى تقاطع المحاور بالنقطة الأصل
(طول القطعة [اب] وحدة الطول على المحور (اب)، كما أن طول القطعة [ات] وحدة الطول على المحور (ات))
نقول أن المستوى منسوب إلى معــلم متعامد
نرمز لمعلم في المستوى بالرمــز : ( ا ؛ب ؛ ت)
نسمي المستقيم (اب) : محــور الأفاصيل
نسمي المستقيم (ات) : محــور الأراتيب

إذا كان اب = ات نقول أن المستوى منسوب إلى معــلم ممنظم و متعامد

كل نقطة ن من المستوى مرتبطة بعددين يسميان إحداثيتي النقطة: الإسقاط العمودي للنقطة ن على محور الفواصل و يسمى أفصول النقطة ن، و الإسقاط العمودي للنقطة ن على محور الأراتيب و يسمى أرتوب النقطة ن٠ و نكتب: ن( س ؛ ص)٠

معادلة الخط المستقيم

لكل خط مستقيم ( م ) في المستوى منسوب إلى معــلم توجد علاقة تربط بين الإحداثي السيني والإحداثي الصادي للنقط الواقعة عليه و هذه العلاقة معادلة من الدرجة الأولى ذات مجاهيل إحداثية، حلها يمثل ذلك المستقيم ونكتبها بالصورة العامة : 
أ ص + ب س + جـ  = 0،   حيث أ، ب، جـ  أعداد حقيقية معلومة ( أ، ب) ≠ (0، 0)    
تسمى المعادلة الديكارتية للمستقيم ( م ) الموجه بالمتجهة (– ب، أ)
(– ب، أ) تسمى المتجه الموجه للمستقيم ( م )

من أجل كل نقطة هـ  و نقطة جـ  من المستقيم (م) فإن المتجهة متجهة موجه للمستقيم (م)


ملاحظة1:
في المستوى منسوب إلى معــلم الصورة العامة لمعادلة خط مستقيم تُكتب على الشكل:
أ ص + ب س + جـ  = 0،   حيث أ، ب، جـ  أعداد حقيقية معلومة ( أ، ب) ≠ (0، 0) 

- إما الخط المستقيم موازي لمحور الأراتيب، و في هذه الحالة تُكتب معادلته على الشكل:  س = أ ، حيث أ عدد معلوم.
- إما الخط المستقيم غير موازي لمحور الأراتيب، و في هذه الحالة تُكتب معادلته على الشكل:  ص = أ س + ب   حيث أ ، ب  عددان حقيقيان. العدد أ يسمى ميل المستقيم أو المعامل الموجه للمستقيم، و العدد ب يسمى الأرتوب عند الأصل.

ملاحظة2:
- ميل المستقيم ( م ) = التغير في الإحداثيات الصادية ÷ التغير في الإحداثيات السينية
- ميل المستقيم ( م ) = ضل الزاوية بين محور الأفاصيل و المستقيم ( م )
- مستقيمان متوزيان لهم نفس الميل

مثال1: 
جد معادلة المستقيم الذي يمر بالنقطة ن ( 1 ، 3 ) والنقطة د ( 2 ، 5 ).

الحل :
أولا : نوجد الميل
ثانيا: نختار أحد النقطتين ونعوض في المعادلة

مثال2: 
جد معادلة المستقيم الذي يمر بالنقطة ن ( 2 ، 3 ) والنقطة د ( 2 ، 5 ).

الحل :
النقطة ن و النقطة د لهما نفس الأفصول ألا و هو العدد 2، إذن معادلة المستقيم المار من النقطة ن و النقطة د هي:  س = 2

معادلة مستقيم بمعرفة نقطة تقع عليه ومستقيم موازي له
مثال:

معادلة مستقيم بمعرفة نقطة تقع عليه ومستقيم عمودي عليه
مثال:

معادلة مستقيم بمعرفة كلٍ من الجزء المقطوع من المحورين : السيني وَ الصادي
مثال:

عموميات حول الدوال



المثال الأول: عندنا علاقة نرمز لها مثلا بِـ عـا تربط كل عنصر من المجوعة فـ = {1 ، 2 ، 3 ، 4 ، 5 ، 6} (تدعى المنطلق) عنصرا واحدا وواحدا فقط من المجموعة قـ = {ا ٬ ب ٬ ج ٬ ح ٬ خ } (تدعى المستقر)٠ تسمى هذه العلاقة تطبيق، ونرمز له بِـ عـا : فـ ← قـ
العنصر ب يسمى صورة العنصر 2 بالتطبيق عـا
العنصر 2 يسمى سابق العنصر ب بالتطبيق عـا

المثال الثاني: عندنا علاقة نرمز لها مثلا بِـ هـا تربط كل عنصر من المجوعة فـ بعنصر على الأكثر من المجموعة قـ
(العنصر 4 ليس له صورة) )٠ تسمى هذه العلاقة دالة، ونرمز له بِـ هـا : فـ ← قـ
العنصر ج يسمى صورة العنصر 3 الدالة هـا
العنصر 3 يسمى سابق العنصر ج الدالة هـا

تعريف:
التطبيق هو كائن رياضي يمثل علاقة تربط بكل عنصر يسمى المتغير من مجموعة تدعى المنطلق عنصرا واحدا وواحدا فقط من مجموعة تدعى المستقر.

تعريف:
الدالة أو التابع هو كائن رياضي يمثل علاقة تربط بكل عنصر يسمى المتغير من مجموعة تدعى المنطلق بعنصر على الأكثر من مجموعة تدعى المستقر.

نرمز للدوال و التطبيقات عادة بالحروف د، ذ، ر، ز، عـا، غـا، هـا.... و للمتغيرات بِالحروف ش، س، ص، ض،... و للدالة و التطببيق عـا من المجوعة ك إلى المجموعة ل للمتغير س، بِـ
                                                      عـا : ك ← ل
                                                            س ↤ عـا(س)

عـا(س) تُقرأ عا لِـ س العنصر عـا(س) يسمى صورة العنصر س بالدالة عـا
العنصر س يسمى سابق العنصر عـا(س) بالدالة عـا

نكتب مثلا الدالة العددية هـا للمتغير الحقيقي س ( منطلقها و مستقرها مجموعة الاعداد الحقيقية): التي تربط بكل عدد حقيقي س، العدد الحقيقي  2س :
                         هـا: حـ ← حـ
                              س ↤ هـا(س) = 2س

أو باختصار الدلة العددية هـا المعرفة بِـ: هـا(س) = 2س

أمثلة لدوال معرفة بمعادلات جبرية:
عـا(ش) = 5ش – 1، دالة عددية للمتغير الحقيقي ش
عـا(ش)= ش² + 7ش + 1، دالة عددية للمتغير الحقيقي ش

أمثلة من الهندسة:
الإنعكاس (الهندسة)
- ط نقطة من المستوى خارج المستقيم (هـ و)
يتم إسقاط خط عمودي على الخط (هـ و) المستعمل كمحور الإنعكاس، ثم مد الخط بشكل مستقيم في الجهة الأخرى من المحور وبنفس المسافة٠
النقطة التي نصل إليها تسمى صورة النقطة ط بالإنعكاس عن المستقيم (هـ و))٠
- ط نقطة من المستقيم (هـ و)
إذا كانت النقطة ا تنتمي إلى محور الإنعكاس (أي المستقيم (هـ و)) فإن صورتها هي نفسها٠



تمرين تطبيقي:
نعتبر الدالة العددية عـا(ش) = ش² + 4ش – 1
أحسب صورة العدد 0
حدد سوابق العدد 5
أحسب صورة 1
حدد سوابق العدد –1
حدد صورة العدد –1

مجال تعريف دالة رياضية، مدى دالة رياضية
مجال تعريف دالة رياضية هو مجموعة جزئية من المنطلق، مجموعة العناصر التي لها صورة فى المستقر. 
مدى دالة رياضية هو مجموعة جزئية من المستقر، مجموعة القيمات المحتمل خروجها كناتج للدالة بعد التعويض بالقيم الخاصة بمجال الدالة (مجموعة القيم الفعلية للدالة)٠ 

مثال:
نعتبر الدالة نعتبر الدالة عـا المعرفة بالرسم البياني التالي المعرفة بالرسم البياني التالي

مجال تعريف الدالة نعتبر الدالة عـا {1 ، 2 ، 3 ، 5 ، 6} ٠
مدى الدالة عـا {ا ٬ ب ٬ ج ٬ خ } ٠

مثال:
مجموعة تعريف الدالة العددية د للمتغير الحقيقي ش المعرفة بما يلي: عـا(ش) = جذر(س)، هي مجموعة الأعداد الحقيقية الموجبة حـ+
مجموعة تعريف دالة المقلوب، هي مجموعة الأعداد الحقيقية الغير منعدمة حـ*

تمرين تطبيقي:
حدد مجموعة تعريف الدالة العددية المعرفة بما يلي: عـا(س) = جذر(س+1)

تركيب دالتين

تعريف:
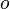
لتكن ك،ل،ي ثلاثة مجموعات٠  لتكن الدالتين د : ك ← ل  و ر: ل ← ي٠ نعرف تركيب الدالة د بالدالة ر و نكتب ر د
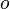
بِـ: من أجل كل س من ك، ر د(س) = ر(د(س))٠
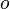
ننتج إذن دالة جديدة د ر: ك ← ي٠ و نقرأ ر تركيب د أو ر بعد د٠

مثال:
نعتبر الدالة العددية د(س) = س²  + 5
نعتبر الدالة العددية  ر(س) = 4س – 1
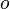
ر د(س) = ر(د(س)) = ر(س2 + 5) = 4(س² + 5) – 1 = 4س2 + 19
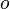
د ر(س) = د(ر(س)) = ر(4س – 1) = (4س – 1)² + 5
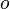
د د(س) =.....
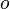
ر ر(س) = ....

تطبيق تقابلي، التقابل العكسي

تعريف:
يكون التطبيق تقابلا إذا كان لكل عنصر من المجموعة المستقر،هناك سابق  وحيد من المجموعة المنطلق٠ أي  أنها تطبيق تبايني (العناصر في المستقر لا ترتبط بعنصرين مختلفين في المنطلق بالتطبيق) وفي نفس الوقت تطبيق شمولي (لكل عنصر من المجموعة المستقر، هناك سابق من المجموعة المنطلق بالتطبيق)٠ 

أي يكون التطبيق د : ك ← ل، تطبيق تقابلي إذا تحقق الشرط التالي: من أجل كل ص من ل يوجد سابق وحيد من ك،
بحيث: د(س) = ص٠

خاصية:
ليكن د : ك ← ل، تطبيق تقابلي، التطبيق الذي يربط بكل عنصر من ل بسابقه (الوحيد) بالتطبيق د، تطبيق تقابلي يسمى التطبيق العكسي لِلتطبيق د أو التقابل العكسي لِلتطبيق د ونرمز له د^-1 ٠

بالأسود الدالة س ↤ د (س)، بالأخضر دالتها العكسية د(س) ↤ س.
من أجل كل س من ك، د^-1 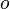د(س) = س
من أجل كل س من ل، د 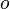د^-1(س) = س

التمثيل المبياني وتغيرات الدوال

التمثيل المبياني




لتكن ها دالة عددية، و (ا ؛ ب ؛ ت) معلما للمستوى٠

التمثيل المبياني للدالة ها، أو منحنى الدالة ها، هو مجموعة نقط المستوى ن(س ؛ ص) بحيث س تنتمي لِمجموعة تعريف الدلة ها، و ص= هـا(س)٠

تغيرات الدوال

تدعى الدالة العددية هـا المعرفة على مجموعة جزئية من الأعداد الحقيقية دالة تصاعدية (↖) إذا كانت تحافظ على الترتيب٬ أي لكل س ≤ ش يتحقّق أيضًا هـا(س) ≤ هـا(ش)، (أنظر رسم 1)٠

تدعى الدالة العددية هـا المعرفة على مجموعة جزئية من الأعداد الحقيقية دالة تنازلية (↙) إذا كانت تعكس آلترتيب٬ أي لكل س ≤ ش يتحقّق أيضًا هـا(س) ≥ هـا(ش)، (أنظر رسم 2)٠




مثال:
نعتبر التمثيل المبياني للدالة العددية هـا للمتغير الحقيقيقي س التلي



الدالة العددية هـا دالة تنازلية من أجل كل س ≤ 3 (أي في المجال [3 ٬ +∞[)، و تصاعدية من أجل كل س ≥ 3 (أي في المجال
]–∞ ٬ 3])٠ و نلخص هذا كما يلي



كيف نتعرف على تغيرات الدوال جبريا؟
نعتبر الدالة العددية عـا للمتغير الحقيقيقي س المعرفة على مجموعة جزئية من الأعداد الحقيقية
للتعرف عن تغيراتها في مجال ما من مجموعة تعريفها ندرس إشارة النسبة: (عـا(س) – عـا(ص)) ÷ (س – ص)
من أجل كل س، ص، س≠ ص من المجال٠
إذا كانت هذه النسبة موجبة في مجال ما، فالدالة تحافظ على الترتيب أي تصاعدية (في المجال الذي تتحقق فية إشارة النسبة)٠
و إذا كانت هذه النسبة سالبة في مجال ما، فالدالة تعكس الترتيب أي تنازلية (في المجال الذي تتحقق فية إشارة النسبة)٠

تمرين تطبيقي:
ادرس تغيرات الدوال التالية
الدالة العددية عا(س) = 4ش – 1
الدالة العددية عا(س) = ج ش – 1 ، حيث ج عدد حقيقي معلوم لا يتعلق بالمتغير
الدالة العددية عا(س) = ش2 ، في مجموعة الأعداد الحقيقية الموجبة، حـ+
الدالة العددية عا(س) = ش2 ، في مجموعة الأعداد الحقيقية

دوال ابتدائية

الدالة الخطيــــة

تعريف:
أ عدد معلوم، العلاقة التي تربط العدد س بالعدد أ س تسمى الدالة الخطية ذات المعامل أ٠ أي الدالة الخطية هي دلة معرفة كالتالي:
                                            هـا: حـ ← حـ
                                                 س ↤ هـا(س) = أ س
بحيث أ عدد معلوم٠

مثال :
هـا(س) = 2س

التمثيل المبياني لدالة خطية

نعتبر الدالة الخطية المعرفة كالتالي:
                                            عـا: حـ ← حـ
                                                س ↤ هـا(س) = أ س
بحيث أ عدد معلوم٠

مِن دراسة إشارة النسبة: (عـا(س) – عـا(ص)) ÷ (س – ص) من أجل كل س، ص، س≠ ص من مجموعة الأعداد الحقيقية، حـ ٠
نٌبيِّن الخاصية التالية:

خاصية:
التمثيل المبياني لدالة خطية في المستوى منسوب إلى معلم متعامد، هو مستقيم يمر من أصل المعلم٠
الدالة الخطية دالة تصاعدية إذا كان المعامل جـ عدد موجب، و تكون تنازلية إذا كان المعامل جـ عدد سالب٠

الدالة التآلفيــــة

تعريف:
أ، ب عددان معلومان، العلاقة التي تربط العدد س بالعدد أ س + ب تسمى الدالة التآلفيــــة ذات المعامل  أ٠ أي الدالة التآلفيــــة هي دلة معرفة كالتالي:
                        هـا: حـ ← حـ
                             س ↤ هـا(س) = أ س + ب
بحيث أ، ب عددان معلومان٠

مثال:
هـا(س) = 2 س + 1

التمثيل المبياني لدالة التآلفيــــة

نعتبر الدالة التآلفيــــة المعرفة كالتالي:
                                               عـا: حـ ← حـ
                                                    س ↤ هـا(س) = جـ س + خـ
بحيث جـ، خـ عددان معلومان٠

مِن دراسة إشارة النسبة: (عـا(س) – عـا(ص)) ÷ (س – ص) من أجل كل س، ص، س≠ ص من مجموعة الأعداد الحقيقية، حـ ٠
نٌبيِّن الخاصية التالية:

خاصية:
التمثيل المبياني لدالة تآلفيــــة في المستوى منسوب إلى معلم متعامد، هو مستقيم٠
الدالة التآلفيــــة دالة تصاعدية إذا كان المعامل جـ عدد موجب، و تكون تنازلية إذا كان المعامل جـ عدد سالب٠ 

دراسة الدوال الحدودية من الدرجة الثانية



الشلجم أو اللفت



تعريف:
الدالة الحدودية من الدرجة الثانية هي التطبيق الذي يربط بكل عنصر ش من مجموعة الاعداد الحقيقية بالعدد الحقيقي عـا(ش)=ج ش² + ح ش + خ ، حيث ج، ح، خ أعداد حقيقية معلومة لا تتعلق بالمتغير ش، ج عدد غير منعدم
أي الدالة المعرفة كالتالي
                               عـا: حـ ← حـ
                                    س ↤ عـا(ش)=ج ش² + ح ش + خ
بحيث ج٬ ح٬ خ أعداد معلومة٠

بصفة عامة يمكن كتابة د(ش) على الشكل التالي: عـا(ش) = ج(ش + ح÷2ج)² + خ – ح² ÷ 4ج 


التمثيل المبياني لدالة حدودية من الدرجة الثانية

نعتبر الدالة الحدودية من الدرجة الثانية المعرفة كالتالي
                                                                    عـا: حـ ← حـ
                                                                         س ↤ عـا(ش)=ج ش² + ح ش + خ
بحيث ج٬ ح٬ خ أعداد معلومة٠

مِن دراسة إشارة النسبة: (عـا(س) – عـا(ص)) ÷ (س – ص) من أجل كل س، ص، س≠ ص من المجال [–ح÷2ج ٬ +∞[، و المجال ]–∞ ٬ –ح÷2ج]٠
نٌبيِّن الخاصية التالية

خاصية:
لتمثيل المبياني في المستوى منسوب إلى معلم متعامد للدالة الحدودية من الدرجة الثانية المعرفة بِـ عـا(ش)=ج ش² + ح ش + خ، قطع مكافئ رأسه النقطة ذات الأفصول –ح÷2ج٠ على الشكل الموضح: منحنى متناظر حول المحور ش = –ح÷2ج، رأسه النقطة ذات الأفصول –ح÷2ج٠






دراسة دالة المقلوب


تعريف:
دالة المقلوب هي التطبيق الذي يربط بكل عنصر ش من مجموعة مجموعة الأعداد الحقيقية الغير منعدمة حـ* بالعدد الحقيقي
بالعدد الحقيقي الغير منعدم عـا(ش)= 1÷ ش ٠
أي الدالة المعرفة كالتالي
                               هـا: حـ* ← حـ
                                    س ↤ هـا(س) = 1÷ س

التمثيل المبياني لدالة المقلوب

مِن دراسة إشارة النسبة: (عـا(س) – عـا(ص)) ÷ (س – ص) من أجل كل س، ص، س≠ ص من المجال ]0 ٬ +∞[، و المجال ]–∞ ٬ 0[٠
نٌبيِّن الخاصية التالية

خاصية:
دالة المقلوب دالة تنازلية في المجالين ]0 ٬ +∞[، و المجال ]–∞ ٬ 0[ ٠
التمثيل المبياني للدالة المقلوب في المستوى منسوب إلى معلم متعامد منحنى متناظر بالنسبة لأصل المعلم، على الشكل الموضح٠



التوابع المثلثية

الراديان
الراديان (Radian) هي وحدة قياس للزوايا المستوية وهي الوحدة الرسمية المعتمدة ضمن النظام الدولي للوحدات المستخدمة في الرياضيات والفيزياء

"في المستوى الأقليدي" النسبة بين محيط الدائرة وقطرها ثابت رياضي (عدد حقيقي لا يتغير مع تغيير قطرالدائرة) نرمز له بالحرف ط أو π  بالحرف اليوناني

تعريف:
الراديان (واحد) هو قياس زاوية تحدد قوساً (دائريا) طوله مساوي لشعاع الدائرة



العلاقة المستعملة للتحويل بين الوحدتين الدرجة و الرديان هي
( راديان = 180 درجة π) ط رديان = 180 درجة
أي راديان واحد يساوي تقريبا 57،29578 درجة

ملاحظة:
بشكل عام نكتب الزاوية بدون أي علامة، و يقصد أن القيمة هي بالراديان

الدائرة المثلثية

تعريف:
الدائرة المثلثية (دائرة الوحدة) هي دائرة في المستوى الأقليدي منسوب الى معلم متعامد ممنظم (مدرج)، مركزها أصل المعلم و شعاعها يساوي الواحد، حيث الاتجاه الموجب هو اتجاه عكس عقارب الساعة



التوابع المثلثية

تعرفنا في الدرس السابق (أول عناصر الهندسة، حقائق عن المثلثات و الدوائر) عن الدوال المثلثية للزوايا من 0 إلى 90 درجة، على أنهم نسب بين ضلعين في مثلث قائم الزاوية٠

دائرة الوحدة ستمكننا بتوسيع تعريفنا ليشمل كل القيم الحقيقية للزوايا٠

نعتبر المستوى منسوب إلى معلم (ا ؛ ب ؛ ت) ممنظم و متعامد٠



كل نقطة ن من دائرة الوحدة، تشكل زاوية رأسها النقطة (0، 0) و ضلعيها محور الأفاصيل الموجب و الشعاع الذي مبدأ النقطة (0، 0) إلى النقطة ن، حيث الاتجاه الموجب هو اتجاه عكس عقارب الساعة. س قياس هذه الزاوية يساوي طول القوس المقابل لها٬ و محصور بين 0 و 2ط

وعكسيا كل عدد حقيقي س محصور بين 0 و 2ط يحدد نقطة وحيدة ن من الدائرة بحيث قياس الزاوية هو العدد س

تعريف
جيب تمام العدد الحقيقي س هو أفصول النقطة ن، أي الإسقاط العمودي للنقطة ن على محور الفواصل، و نرمز له بِـ تجب(س)٠
جيب العدد الحقيقي س هو أرتوب النقطة م، أي الإسقاط العمودي للنقطة م على محور الأراتيب، و نرمز له بِـ جب(س)٠



بعض الزوايا الشائعة مع قيم جيب التمام و الجيب و الظل المناظرة لها٠



دراسة التوابع المثلثية
........................