تمارين
تمرين17
لديك مجموعة من المثلثات قوائم الزاوية وعُلِمَ في كل حالة منها طولي ضلعين كما هو مبين في الجدول التالي، احسب طول الضلع الثالث
بين أن القطعة [ا ج] قطر الدائرة المحيطة بالمثلث التاني٠
تمرين18
أ ب ج مثلث حيث
طول [أ ب] = 6 سنتيمتر
طول [ب ج] = 8 سنتيمتر
طول [أ ج] = 10 سنتيمتر
بَيِّن أن المثلث أ ب ج قائم الزاوية
طول [أ ج] = 10 سنتيمتر
بَيِّن أن المثلث أ ب ج قائم الزاوية
تمرين19
أ ب ج مثلث حيث
أ ب ج مثلث حيث
طول [أ ب] = 3 سنتيمتر
طول [ب ج] = 5 سنتيمتر
طول [أ ج] = 8 سنتيمتر
هل المثلث أ ب ج قائم الزاوية ؟
طول [أ ج] = 8 سنتيمتر
هل المثلث أ ب ج قائم الزاوية ؟
تمرين20
أ ب ج مثلث قائم الزاوية في أ
بيّن أن: جب2 (هـ) + تجب2 (هـ) =1
تمرين21
دائرة الوحدة
و أن: جب2 (س) + تجب2 (س) =1 ، من أجل كل عدد حقيقي س
تمرين22
أ ب ج مثلث قائم الزاوية في أ حيث
طول [أج] = 10 سنتيمتر
قياس الزاوية ب = 60 درجة
احسب طول [ب ج]
تمرين23
الدرس
أول عناصر الهندسة
النقطة
في الهندسة الرياضية،
النقطة عبارة عن كائن رياضي عديم الأبعاد يمثل مفهوما أساسيا في الهندسة
الرياضية. تتميز النقطة بأنها تملك موقعا في الفراغ لكن بدون حجم ومساحة
ولا أبعاد فهي تمثل معلومات عن الموقع فقط دون أي خواص رياضية أخرى٠
المستقيم
المستقيم خط مستقيم يمتد إلى ما لا نهاية من الجهتين٠
نرمز للمستقيم الدي يمر بالنقطة ا والنقطة ب بالرمز: (ا ب)٠
نصف مستقيم
نصف مستقيم هو جزء من خط مستقيم يكون محدودا من جهة واحدة فقط
نصف مستقيم لا يمكن قياس طوله
الترقيم
الترقيم
نرمز للمستقيم المحدود بالنقطة ا، و يمربالنقطة ب بالرمز: [ا ب)٠
القطعة المستقيمة
القطعة
المستقيمة هي جزء من خط مستقيم محددة بنقطتين تسميان نقطتي النهاية وتضم
جميع النقاط الواقعة على المستقيم بين هاتين النقطتين٠
القطعة هي جزء من خط مستقيم محدود من طرفيه و يمكن قياس طولها٠
القطعة هي جزء من خط مستقيم محدود من طرفيه و يمكن قياس طولها٠
الترقيم
نرمز للقطعة المستقيمة التي تمر بالنقطة ا والنقطة ب بالرمز: [ أ ب ] أو [ ب أ ]، والنقطتان أ وَ ب هما
طرفاها٠
و نرمز لطول القطعة المستقيمة [ا ب] بالرمز: ا ب
الزاوية
الزاوية هي الشّكل الهندسي الناتج عن التقاء شعاعين بنقطة بدايتهما تسمى رأس الزاوية.

التعامد
يعتبر مستقيمان متعامدين على بعضهما إذا شكلا زوايا متجاورة متطابقة. تسمى زوايا قائمة (قياس الزاوية القائمة يساوي 90° درجة)٠
جميع الزوايا المكونة من تعامد خطين مستقيمين هي زوايا قائمة. وبالعكس فإن أي
خطين مستقيمين يشكلان زوايا قائمة فهما متعامدان٠
يرمز لعملية التعامد بين خطين بالعلامة 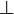
التوازي
يعتبر مستقيمان (في المستوى) متوازيين إذ استحالة التقاءهما٠
يرمز لعملية التوازي بين خطين بالعلامة 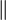
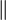
إذا كان مستقيمان متعامدان، فكل مستقيم موازي لأحدهما يكون عموديا على الآخر.
إذا كان مستقيمان متوازيان فكل مستقيم عمودي على أحدهما يكون عموديا على الآخر.
المسافة بين نقطة وخط مستقيم
ط نقطة من المستوى٬ أقرب مسافة تفصل النقطة ط عن الخط المستقيم (م) هي طول القطعة [ط ا]٠ تسمى المسافة أو (المسافة الدنيا) بين النقطة ط و الخط المستقيم (م)، و النقطة ا تسمى الإسقاط العمودي للنقطة ط على المستقيم (م)٠
تعريف
المسافة أو (المسافة الدنيا) بين نقطة ما من المستوى و خط مستقيم ما من المستوى
هي أقرب مسافة تفصل النقطة عن الخط المستقيم٠
الدائرة
الدائرة
هي المحل الهندسي للنقاط المتصلة ببعضها البعض والواقعة في المستوى من على
بعد ثابت من نقطة ثابتة ما، والتي تسمى مركز الدائرة. المسافة الفاصلة بين
مركز الدائرة وأي نقطة منها تسمى شعاعا أو نصف قطر٠
المماس للدائـرة
المماس هو ذلك المستقيم الذي يلاقي الدائرة في نقطة واحدة تعرف بنقطة تماسه معها (نقطة التماس)٠
المماس هو ذلك المستقيم الذي يلاقي الدائرة في نقطة واحدة تعرف بنقطة تماسه معها (نقطة التماس)٠

المماس للدائـرة يكون عمودياً على نصف القطر المار بنقطة التماس٠
المستقيم العمودي على نصف القطر في دائرة عند نهايته يكون مماساً للدائرة٠
المثلث
المستقيم العمودي على نصف القطر في دائرة عند نهايته يكون مماساً للدائرة٠
المثلث
تعريف المثلث المثلث هو أحد الأشكال الأساسية في الهندسة، وهو شكل ثنائي الأبعاد مكون من ثلاثة رؤوس تصل بينها ثلاثة أضلاع، وتلك الأضلاع هي قطع مستقيمة٠
أنواع المثلثات
مثلث متساوي الأضلاع: هو مثلث جميع أضلاعه متساوية٠
مثلث متساوي الضلعين: ويسمى أيضا متساوي الساقين، هو مثلث فيه ضلعان متساويان٠
مثلث قائم: له زاوية قياسها 90 درجة (زاوية قائمة)، يدعى الضلع المقابل للزاوية القائمة بالوتر، وهو أطول أضلاع هذا المثلث٠
مثلث متساوي الضلعين: ويسمى أيضا متساوي الساقين، هو مثلث فيه ضلعان متساويان٠
مثلث قائم: له زاوية قياسها 90 درجة (زاوية قائمة)، يدعى الضلع المقابل للزاوية القائمة بالوتر، وهو أطول أضلاع هذا المثلث٠
حساب زوايا المثلث الداخلية: مجموع قياسات زوايا المثلث الداخلية تساوي 180 درجة٠
حساب مساحة المثلث: المساحة = ½ القاعدة × الارتفاع
نقط ومستقيمات ودوائر مرتبطة بالمثلث
المتوسطات العمودية
تعريف
المتوسط العمودي لمثلث هو مستقيم يمر من أحد أضلاع المثلث في منتصفه ويكون عمودياً عليه
خاصية تتقاطع المتوسطات العمودية الثلاثة في مركز الدائرة المحيطة بالمثلث وهي الدائرة التي تمر من رؤوس المثلث ويكون تقاطع متوسطين عموديين فقط كافياً لمعرفة مركز هذه الدائرة
المثلث القائم و الدائرة المحيطة به
تعريف
المتوسط العمودي لمثلث هو مستقيم يمر من أحد أضلاع المثلث في منتصفه ويكون عمودياً عليه
خاصية تتقاطع المتوسطات العمودية الثلاثة في مركز الدائرة المحيطة بالمثلث وهي الدائرة التي تمر من رؤوس المثلث ويكون تقاطع متوسطين عموديين فقط كافياً لمعرفة مركز هذه الدائرة
المثلث القائم و الدائرة المحيطة به
خاصية
إذا كان مركز الدائرة المحيطة بالمثلث على ضلع من أضلاع المثلث فإن الزاوية المقابلة لهذا الضلع تكون قائمة أي المثلث قائم ٬ كما أن إذا كان المثلث قائم فإن مركز الدائرة المحيطة به هو منتصف وتره٠
الارتفاعات
تعريف
الارتفاع هو مستقيم يمر براّس من رؤوس المثلث ويكون عمودياً غلى الضلع المقابل للرأس
خاصية
يمثل الارتفاع البعد بين الرأس والضلغ المقابل له كما تتقاطع الارتفاعات في نقطة تسمى مركز قائم
منصفات الزوايا
تعريف منصف الزاوية هو مستقيم يمر من أحد رؤس المثلث ويقسم الزاوية إلى نصفين
خاصية
تتقاطع المنصفات الثلاثة في مركز الدائرة المحيطة بالمثلث وهي الدائرة التي تمس أضلاع المثلث الثلاثة ويكون تقاطع منصفين فقط كافياً لمعرفة مركز هذه الدائرة
المتوسطات
تعريف
المتوسط هو قطعة مستقيم تنطلق من أحد رؤس المثلث وتمر من منتصف الضلع المقابل لهذا الرأس
خاصية
تتقاطع المتوسطات الثلاثة في نقطة تسمى مركز ثقل المثلث ويكون تقاطع متوسطين فقط كافياً لمعرفة مركز الثقل
كما يكون البعد بين رأس المثلث ومركز الثقل مساوياً لـ
 من طول المتوسط الصادر من ذلك الرأس
من طول المتوسط الصادر من ذلك الرأس
مبرهنة فيثاغورس
خاصية مبرهنة فيثاغورس: في المثلث ا ب ت القائم الزاية في النقطة ا، مربع طول الوتر [ب ت] يساوي مجموع مربعي طولي الضلعين القائمين [ا ب] ، [ا ت]٠
أي : ب ت2 = ا ب2 + ا ت2
مبرهنة فيثاغورس العكسية
خاصية
في مثلث، إذا كان مربع طول أطول ضلع يساوي مجموع مربعي طولي الضلعين الآخرين، فإن هذا المثلث قائم الزاوية. الزاوية القائمة هي الزاوية المقابلة لأطول ضلع، والضلع الأطول هو الوتر٠
الحساب المثلثي، تعميم نظرية فيثاغورث
الحساب المثلثي
في المثلث أ ب ج القائم الزاوية في أ
جيب التمام الزاوية هـ = الضلع المجاور للزاوية مقسوما على الوتر
جيب الزاوية هـ = الضلع المقابل للزاوية مقسوما على الوتر
ظل الزاوية هـ = الضلع المقابل للزاوية مقسوما على الضلع المجاور لها
كما أن: ظل الزاوية = جيب الزاوية مقسوما جيب تمام الزاوية
من خلال التعريفات يمكن أن نُبيِّن أن
جيب و جيب تمام زاوية ما عددان بين 0 و 1 -
ظل الزاوية = جيب الزاوية مقسوما جيب تمام الزاوية -
تجب(هـ) = جب(90 – هـ)٠ -
خاصية
جب(هـ) (جيب) و تجب(هـ) (جيب تمام) قيمها محصورة بين 0 و 1
جب2 (هـ) + تجب2 (هـ) =1
مثال
في المثلث ا ب ت القائم الزاوية في ا
طول [ا ت] = 15 سنتيمتر
طول [ا ب] = 5 سنتيمتر
طول [ا ت] = 15 سنتيمتر
طول [ا ب] = 5 سنتيمتر
فيكون ظل الزاوية ب: ا ت ÷ ا ب = 15÷ 5 = 3
عند معرفة قيم ضلعين أو قيم ضلع وزاوية، يمكن إيجاد قيم باقي عناصر المثلث (زوايا واضلاع) باستخدام قوانين الجيب وقوانين جيب تمام وقوانين ظل الزاوية و الدوال العكسية
|
مثال
فيكون ظل الزاوية ب: ا ت ÷ ا ب = 15÷ 5 = 3
مبرهنة الكاشي (تعميم نظرية فيثاغورث): مربع طول الضلع يساوي مجموع مربعي الضلعين الآخرين مطروح منه ضعف حاصل ضروب طولي الضلعين الآخرين في جيب تمام "الزاوية المحصورة بينهما"٠
الزوايا المركزية والزوايا المحيطية
1) الزاوية المركزية، الزاوية المحيطية:
تعريف:
الزاوية المركزية هي كل زاوية رأسها مركز دائرة و ضلعاها يقطعان الدائرة.
الزاوية المحيطية هي كل زاوية رأسها ينتمي إلى دارة و ضلعاها يقطعان الدائرة.
نعتبر الشكــل جانبه:
لدينا الزاوية س م ص زاوية مركزية تحصر القوص س ص
لدينا الزاوية س ع ص زاوية محيطية تحصر القوص س ص
لدينا الزاوية س ب ص زاوية محيطية تحصر القوص س ص
حالة خاصة، الزاوية المماسية:
لاحظ الشكــل جانبه بحيث المستقيم (ب ت) مماس للدئرة في النقطة ب
الزاوية ج ب ت زاوية محيطية تحصر القوس ج ب
الزاوية ج ب ت زاوية محيطية تحصر القوس ج ب
3) خصــائص:
تعريف :
تكون زاوية مركزية مرتبطة بزاوية محيطية إذا كانتا تحصران نفس القــوس.
خــاصية :
زاويتان محيطيتان تحصران نفس القوس تكونان مقايستين
قياس زاوية محيطية يساوي نصف قياس الزاوية المركزية المرتبطة بهامثال :
لدينا الزاوية س ع ص زاوية محيطية تحصر القوص س ص
لدينا الزاوية س ب ص زاوية محيطية تحصر القوص س ص
لدينا الزاوية س ب ص زاوية محيطية تحصر القوص س ص
إذن: م = 2 × ع = 2 × ب
حالة خاصة
لاحظ الشكــل جانبه بحيث المستقيم (ب ت) مماس للدئرة في النقطة ب
لدينا: الزاوية ت بج زاوية محيطية تحصر القوس بج
لدينا: الزاوية ت بج زاوية محيطية تحصر القوس بج
alfarjimohammed@gmail.com




















ليست هناك تعليقات:
لا يسمح بالتعليقات الجديدة.